On Hash Functions for the GPU

This blog posts shows how the PCG2D hash function works geometrically. Further, we discuss a quantitative statistical test that may help to optimize parameters as compared to classical pass/fail test suites.

$\def\H{\mathbb{H}} \def\H1{\mathbb{H}^1} \def\N{\mathbb{N}} \def\E{\mathbb{E}} \def\Z{\mathbb{Z}} \def\T{\mathbb{T}} \def\R{\mathbb{R}} \def\C{\mathbb{C}} \def\S{\mathbb{S}} \def\V{\mathbb{V}} \def\HR{\H(\R)} \def\HU{\mathbb{H}^1(\mathbb{R})} \def\SU{\text{SU}(2)} \def\su{\mathfrak{su}_2} \def\SO{\text{SO}(3)} \def\So{\text{SO}(2)} \def\SL{\text{SL}_2(\Z)}$

Pseudo random number generators and hash functions

First, in order to clarify the terminology, I adopt the concept of “wide” vs “deep” pseudo random number generators (prng).¹ A typical prng works by going deep: we iterate the generator with a fixed starting seed, using the output of the last as seed for the next call. In contrast, a hash function is only applied once on a wide range of input values. The output of the hash function should be distributed randomly in the image domain, which usually is the set of 32-bit unsigned integers. This property makes it suitable to be used as a prng that runs on a GPU: For each kernel invocation, we wish to produce a random number independent of the other kernels. The input seed might simply be the thread id. Some prngs, like the LCG, allow to jump ahead² any number of iterations without calculating each intermediate value work, which also allows for a GPU implementation.

Secondly, one may ask what properties a good prng should have. What does random mean? One way to answer is to perform a series of statistical tests, such as those introduced by Knuth³ or Marsaglia.⁴ Usually these tests are qualitative: There is null hypothesis, say, “this prng draws from the uniform distribution”, that is, a random number between 0 and 2^32-1, and a probability is calculated of seeing the output if it were really random. If this probability, called p-value is very small, the null hypothesis is rejected, and the test is failed.

The inner workings of PCG2D

A recent paper by Jarzynski and Olano⁵ benchmarks different GPU hash functions and performs the small/big crush tests from the TestU01 test suite.⁶ The hash functions considered are implemented and visualized on shadertoy.⁷ They also introduce a collection of PCG⁸ variants that do well in both performance and benchmark. Let’s pick up PCG2D which was introduced in that paper:

uvec2 pcg2d(uvec2 v)
{
    v = v * 1664525u + 1013904223u;

    v.x += v.y * 1664525u;
    v.y += v.x * 1664525u;

    v = v ^ (v>>16u);

    v.x += v.y * 1664525u;
    v.y += v.x * 1664525u;

    v = v ^ (v>>16u);

    return v;
}

Let’s study how it works. We will do so geometrically. Input and output is 2-dimensional, and we can consider pcg2d as a function on the discrete 2-torus to itself.$\T^2_{32}:=\Z^2/2^{32}\Z^2$.

We plot the torus as square, where opposite sides are identified or “glued together”.

Suppose the input of the hash functions will be the collection of vectors (x,y) with both x and y ranging between 0 and 1023, a typical range of thread ids for a GPU kernel call. This will define a small square S in the left bottom corner in our discrete 2-torus. A good hash function will redistribute this square among the whole torus.

We start with a vectorized LCG:

v = v * 1664525u + 1013904223u;

Multiplying by 1664525, we scale the square to a square grid. We have an offset, addition by 1013904223, which moves the grid by around a quarter of the torus width $1013904223/(2^{32}-1)\approx 0.24$.

Next we have the two shears,

v.x += v.y * 1664525u;
v.y += v.x * 1664525u;

which takes the matrix form

$$v = NUv \quad\text{ where } U = \begin{bmatrix} 1 & 1664525 \\ 0 & 1 \end{bmatrix} \text{ and } N = \begin{bmatrix} 1 & 0 \\ 16645250 & 1 \end{bmatrix}.$$

The horizontal shear U causes points lying on different heights to become independent from each other, similar the vertical shear N for horizontal lines.

Furthermore, we observe the following expansion: U spreads mass horizontally. N spreads mass vertically. Applying both successively leads to uniform distribution of mass.⁹

This leads to a cross pattern which is made up from cut up diagonal lines of different angle.

The next step permutation is surprisingly important:

v = v ^ (v>>16u);

We can use dyadic decomposition to give some geometric meaning to it. For v=(x,y), the pair of highest bits in each of x and y determines in which quadrant v lies. Then, the next pair of bits gives the sub-quadrant inside it. And so on until we reached the smallest subquadrant consisting of 4 points only. Having a diagonal line pattern, these lowest bits become somewhat deterministic. The xorshift permutation thus combines global position (high bits) to the local position leading to some broken up, zigzag pattern.

Iterating now the two shears, will finally result into a complete scramble except for the three lowest bits. Another xorshift copies the scramble from the high bits to the lowest bits.

We draw this sequence in a miniature model. Instead of using 32 bit integers, we use 11 bits. We start with an initial square of 2^6 width size. We then apply the vectorized LCG. Note that very large values will tile the grid over itself.

We apply the translation, and see the two shears in action. The scramble, as promised, is of dramatic nature.

Monobit test — quantitatively

PCG2D fails 35 of the 160 statistical tests of BigCrush.¹⁰

Let’s consider the simplest test of them all, the monobit test. It is described in Section 2 in a NIST paper introducing a Statistical Test Suite for random bit streams.¹¹

To generate a bitstream from PCG2D we simply concatenate the x and y coordinates of the output, and concatenate all of the outputs of the input sequence

$$(0,0),(1,0),…,(x_{max}-1,0),(0,1),… ,(x_{max}-1,y_{max}-1).$$

Suppose this gives us $n = 2*32*x_{max}*y_{max}$ bits. Attach to each bit value $b_i$ the number $z_i = 2b_i-1$, i.e. 1 if the bit is on and -1 if it is off. Then the sum

$$S_n = z_1+…+z_n$$

should behave like the simple random walk.¹²

In particular, the central limit theorem applies, and $\frac{S_n}{\sqrt{n}}$ should be normally distributed, that is, the distribution should follow the Gaussian bell curve.

What will the statistical test suite do? It will put up the null hypothesis that the bit stream is random, and we are indeed normal. Hence with high probability $S_n$ should lie somewhere inside the big bulge of the bell curve.

Let’s make this quantitative. We will repeat this experiment, producing lots of $S_n$ by offsetting the initial input sequence by $(ax_{max},by_{max})$ for integers a,b.

We thus get empirical samples of $S_n$, and we will compare it against the normal curve using the Kullback-Leibler divergence (KL), also known as cross entropy. To do so, we also discretize the normal curve.

Concretely, this means that we create two histograms, say for m buckets, for both the empirical $S_n$ and for the normal curve, which will provide us with two distributions ${p_i}$ and ${q_i}$. $p_i$ is the number of samples $S_n$ that fall inside the ith bucket divided by the total number of samples. $q_i$ will be the mass below the normal curve bounded by the left and right boundaries of the bucket.

Then,

$KL = \sum_{i=1}^m p_i \log(\frac{p_i}{q_i})$.

This function should be as small as possible, it is zero, for non-zero probabilities, if and only if p agrees with q.

Here is an example histogram for 512 many different samples of $S_n$ and the continuous normal curve plotted over it. The KL was about 0.02.

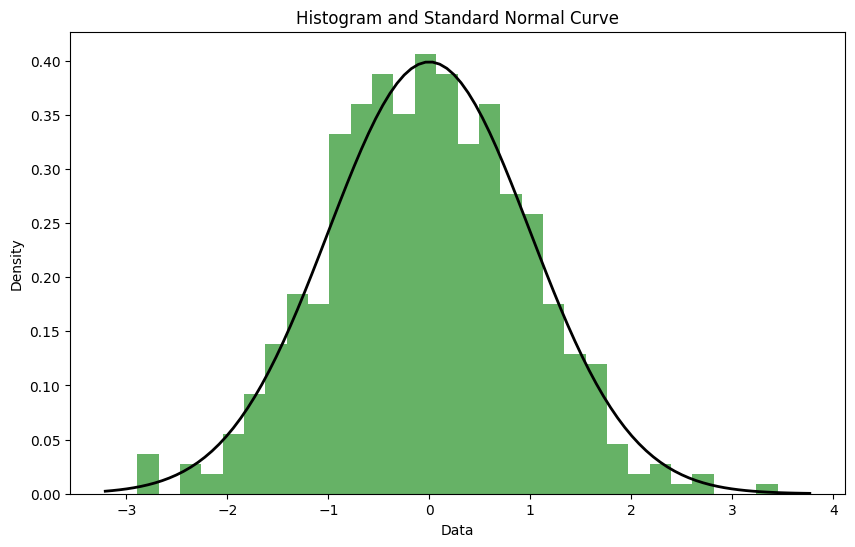
We can calculate a KL value for various parameters of the PCG2d. To plot them, we normalize them to lie between 0 and 1 by dividing by the maximal KL value. Here is a plot where we vary among the first two shears. The final two shears are set to zero to make the result more continuous. Clearly visible are the low quality parameters close to multiples of 2.

In the following plot, we add the second pair of shears. This will avoid parameters that do not behave random whatsoever, but also removes some continuity that was apparent in the previous plot.

PCG3D – random shears?

We finish by mentioning PCG3D, which only fails a single test of BigCrush:

uvec3 pcg3d(uvec3 v) 
{
    v = v * 1664525u + 1013904223u;

    v.x += v.y*v.z;
    v.y += v.z*v.x;
    v.z += v.x*v.y;

    v ^= v >> 16u;

    v.x += v.y*v.z;
    v.y += v.z*v.x;
    v.z += v.x*v.y;

    return v;
}

We will interpret this method from the viewpoint of the PCG paper, which stipulates to use random permutations in the following sense. We assume we have a collection of function $f_a$ parametrized by a scalar $a$. Or put differently, we have a function F which maps scalars to functions, $F:a\mapsto f_a$. These functions are assumed to be invertible and, hence are permutations. Here we take the shears, $U_a = \begin{bmatrix} 1 & a & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$, so that

 v.x += v.y*v.z;

becomes $v=U_{v.z}v$. Similarly, for the other dimensions, so that we interpret

v.x += v.y*v.z;
v.y += v.z*v.x;
v.z += v.x*v.y;

as a sequence of three random shears. This analogy could be made stronger if v.z in $U_{v.z}$ would be replaced by $U_{\text{rng}(v.z)}$ for some scrambler $\text{rng}$.

Source code

The source code is available at https://github.com/reneruhr/gpuhash.

There is a great possibility of directions one could go from here. Adding more statistical tests and implement some machine learning algorithms that will search for the best parameters for example.

1. Nathan Reed: Quick And Easy GPU Random Numbers In D3D11 ↩︎
2. Nathan Reed: Hash Functions for GPU Rendering ↩︎
3. Donald Knuth: The Art of Computer Programming. Volume 2. Seminumerical Algorithms. Chapter 3.3 ↩︎
4. Wikipedia on the Diehard tests ↩︎
5. Journal of Computer Graphics Techniques: Jarzynski and Olano – Hash Functions for GPU Rendering ↩︎
6. https://en.wikipedia.org/wiki/TestU01 ↩︎
7. https://www.shadertoy.com/view/XlGcRh ↩︎
8. Melissa O’Neill – PCG, A Family of Better Random Number Generators ↩︎
9. As a side note we remark that if we were to apply $U_1 = \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix} \text{ and } N_1 = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}$ in a random order, we would also equidistribute. This is one of the landmark results in the theory of representation theory applied to expander graphs. Details can be found in Discrete Groups, Expanding Graphs and Invariant Measures by Alex Lubotzky. ↩︎
10. The statistical tests done are for 1 dimensional prngs. Jarzynski and Olano choose the following method to put higher dimensional prngs into this frame work:
    If the output is in d dimension, it is simply serialized, i.e. if vectors v1,v2,v3 are produced, the test is given v1.x,v1.y,v2.x,v2.y,v3.x,v3.y.
    As input seeds, the sequence 0,1,2,3,… is used. If the input is in d dimensions, Morton ordering is used to construct a d vector from n,..,n+d-1. It seems to be that this additional interleaving might give an additional advantage of the higher dimensional prngs studied in that paper. ↩︎
11. NIST SP 800-22 Rev. 1 A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications ↩︎
12. Wikipedia: 1D Simple random walk ↩︎